用MATLAB写出代码实现工艺约束，如最大最小尺寸约束，特定的形状约束等。

ANSYS 中的拓扑优化可以设置变形量、最小加工尺寸、对称、拔模方向等约束条件

激光粉末床熔合（L-PBF）打印可能遇到的失败包括是零件从基板上切下后的形状变形，以及打印过程中铺粉机构与打印件的碰撞。与其遭受损失，不如利用拓扑优化消除隐患。

案例：拓扑优化应用于 3D 打印中的变形约束

特点：除了全局拓扑优化之外，制定的约束条件可防止过度的零件变形和相关的构建失败，而支撑的合规性会适度增加。

研究团队：荷兰特温特大学、荷兰代尔夫特理工大学

有限元法的增材制造模拟：

打印过程模拟示意图如下

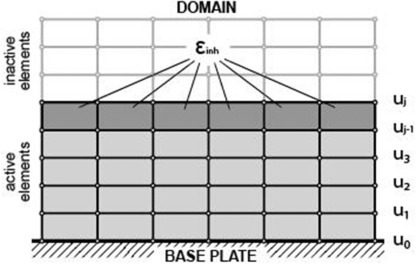
打印是从基板开始的，连接基板节点的位移自由度U0被完全压制。打印到j-1元素层，即（j-1）th步，总的自由度是

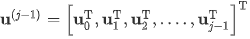
一组新材料层的沉积始于新元素层的激活。新激活行的自由度Uj被添加到当前的自由度集合中

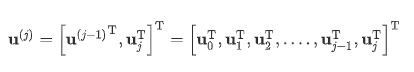
离散化的有限元方程为

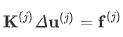
ΔU（j）是j步的位移增量

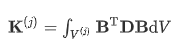
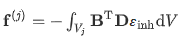
V（j）是当前体积，D是各项同性弹性材料矩阵，B是评估节点位移的应变，εinh是固有应变向量。

在固有应变接近时，由于材料冷却而导致的热收缩是预先计算出来的，其机械当量是以下公式

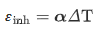
α是热膨胀系数，ΔT是层冷却期间的温度变化。热机械多增量可由单个机械增量代替。

自由度集被划分为抑制的自由度ΔU0和有待确定的

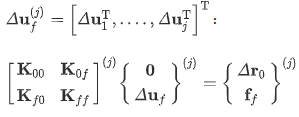
在标准有限元代码中，通常只有Kff（j需要组合，因为已知抑制自由度等于零。

为了计算从基板移除工件的变形，有必要计算基板上的反作用力

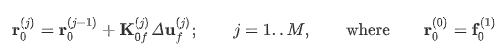
后面添加层的收缩为

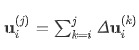
每一步都会执行几何线性分析，这意味着计算出的位移不用更新节点位置。因此，构建阶段的所有层沉积步骤都可以视为独立的线性问题，可以并行解决。

从基板释放后的变形：

构建过程完成后，工件将包含导致反作用力的残余应力r0(M)在底板的抑制自由度中。通过释放受抑制的自由度并将残余应力释放到新的平衡来完成从基板的释放。

释放后，工件应保持由一组静态确定的自由度充分支撑，以抑制刚体运动。为此，对于步骤(M+1)所有自由度u(M)被划分为一组抑制的自由度us(M+1)和其余的uf(M+1)。释放时的失真计算如下

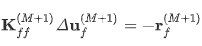
Kff是未压缩自由度相关的刚度矩阵，rf(M+1)是释放基板自由度中的反作用力

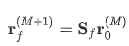
Sf从固定到基板上的自由度中选择，到现在释放。选择的结果是一个长度相同的向量ΔUf(M+1)除了对应的条目，其余条目r0(M)等于零。因为没有激活额外的元素层，自由度总向量ΔU(M+1)与上一个构建步骤ΔU(M)相同。但最后一个构建步骤，刚度矩阵分区Kff(M+1)与Kff(M)不同，所以ΔU(M+1)与ΔU(M)也不同。

为了计算释放时的变形，监测的是抑制基板节点中的反作用力，而不是内部应力。这两种方法是等效的。选择了反作用力矢量选项是因为它为伴随灵敏度计算提供了更简单和更直观的系统描述。只要问题是线性的，所获得的释放时变形值是唯一的。

拓扑优化：

在结构拓扑优化中，最常见的最小化目标是合规性，而允许的材料体积被限制在设计空间的特定百分比。

使用了 SIMP（带约束的固体各向同性材料）方法。设计空间被划分为一个规则的网格，包含Ne相同大小的有限元，每个都有体积V0。设计变量是元素材料密度ρ (0＜ρi≤1，i=1,2……Ne) 描述材料分布。这里ρ=0表示无效，ρ=1表示材料的完全存在。推荐设计ρ等于零或一，单元对刚度矩阵的作用是用约束指数计算的

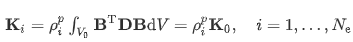
在规定载荷下最小化柔顺度（最大化刚度），并限制最大允许结构体积。规定单元密度的界限，并要求结构与施加的载荷保持平衡。

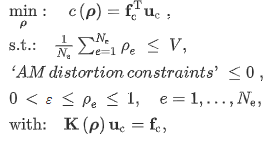
K（ρ）是结构刚度矩阵，fc和uc是零件性能模拟的载荷矢量和位移矢量。

?是一个下界ρ设置以防止奇点，V是允许的最大体积分数。

AM失真约束：

设计的可制造性可能会受到与增材制造相关的变形的影响。本文研究了两个失真约束。第一个是构建过程中的变形，这可能导致铺粉机构与变形产品的灾难性碰撞。第二个是工件从基板上释放后的最终变形，这可能导致产品尺寸超出规格。

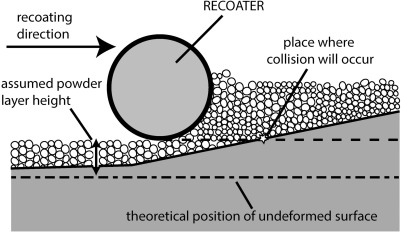
每次沉积新层时，构建板都会降低与层厚度相等的距离，新的粉末层均匀地分布在工作区域上。铺粉机构扫描该区域并扫除多余的粉末，确保均匀恒定的粉末层厚度。如果在正构建方向上过度变形，铺粉机构可能会与零件发生碰撞。

约束方程的为

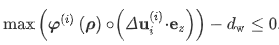
其中乘法ΔUi(i)和ez结果在垂直（z)层位移增量的分量i存放后的顶部节点。符号ο表示 Hadamard 乘积，即两个数组的逐个元素相乘，其结果是一个维数相同的数组。数组包含节点密度，定义为连接到给定节点的当前活动元素的平均密度

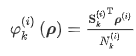
Sk(i)选择已经存放的元素，这些元素连接到节点k，Nk(i)是连接到节点的活动元素的数量K。 这样做是为了只约束实体零件的变形，因为零密度意味着没有材料与节点相关联并且不存在碰撞危险。允许失真dw取决于沉积层厚度t和金属粉末的相对密度ρpwdr

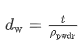
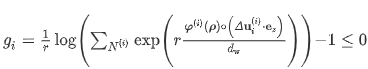
N(i)是ith层节点的数量，r是一个缩放参数。当选择较高的r时该函数更接近于最大函数，但其导数不太平滑。这里假设数组的指数函数给出分量的指数数组。上面方程的约束可以应用于每个单独的层，也可以在所有层上聚合为单个平滑最大函数。在这项工作中，选择了后一个选项。

变形约束：

如下图，理论形状以灰色表示。

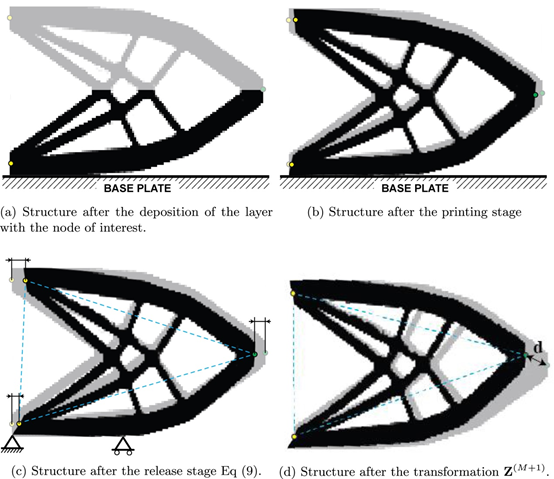
由于连续制造期间的扭曲，理论装配点远离其预期位置。因此需要将所选节点放回其设计的位置。

节点的变形由每个单独的计算步骤的一系列位移增量组成。如果要测量一个节点的变形并相对于其他节点进行约束，则必须在多个节点之间应用转换，其中第一个节点已作为层的一部分沉积. 最终的失真向量按以下形式计算

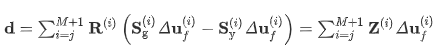
Sg(i)是右侧绿色节点的选择矩阵，Sy(i)是底部组装节点的选择矩阵，并且在减法之后转换整个结构，使得黄色底部节点回到其预期位置。R（i）是旋转结构的旋转矩阵，使得顶部组件节点位移X-component 等于 0。如果黄色节点沉积在受约束的绿色节点之前，它的位移仍然对约束函数有贡献。Z（i）是一个包含上述所有操作的变换矩阵。这个公式可以类似地扩展到 3D 和多个节点。

实际约束gd是一个标量函数

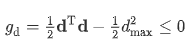
这意味着所考虑节点的变形被限制在球面公差区域内。如果需要一个椭球区域，可以将第一项更改为dTAd，p-norm 可用于盒形区域。

流程：

在每次拓扑优化迭代中，都会执行单独的FEM打印模拟。为此，使用了前面介绍的数值模型。模拟提供了有关变形程度和可能违反打印约束的信息。此外，为了在满足约束条件的同时找到最小化目标函数的设计变量的变化，必须计算这些约束条件对设计密度的敏感性。考虑到设计变量与响应的比例很大，伴随方法是合适的。

将约束函数及其灵敏度并入到拓扑优化算法中。如下图所示，每次优化迭代都需要两次并行数值计算。由于模型的顺序性，AM 模拟及其灵敏度计算是最耗时的。不过这种制造模拟的步骤可以并行，从而可以显著减少总体计算时间。过滤后的密度的敏感度始终转换为未过滤的密度，然后提供给优化器。渐近线用于执行约束优化。最后，进行收敛检查，算法继续进行下一次迭代或停止。

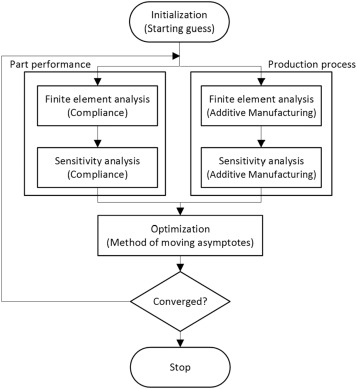
验证阶段：

优化结构为一个一侧固定，另一侧受力的支架。数值算法使用OpenMP并行化。粉末材料为Ti6AL4V。打印层厚50μm。模拟打印元素层厚度1mm，包含50个打印层。

2D示例

1、采用矩形设计域，其离散化为120X80双线性，四边形元素为1X1mm与2X2mm 高斯积分方案。当结构在左侧支撑并且在右侧边缘的中心施加垂直载荷时，结构的柔度最小化。如下图 (a) 具有边界条件的设计域， (b) 在没有打印约束的情况下获得符合性最小化的零件布局。

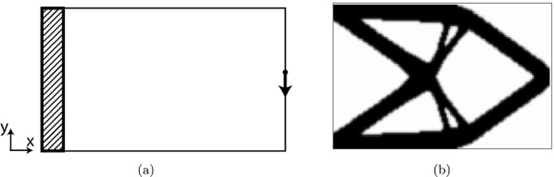
Ti6Al4V材料杨氏模量E=110Gpa，泊松比v=0.342。 规定载荷fc指向负面y-方向的大小为 1000 N。在模拟中假设平面应变变形。最大体积分数设置为 40%。密度过滤器半径设置为 1.5 mm。

规定的固有应变?inh=(0.00598,0,0)，该值对应于Ti6Al4V 从 800 °C 冷却到 150 °C 时的热收缩分量。打印模拟使用每步厚度为 1 mm 的元素层执行，其中包含 20 个打印层，每个打印层的厚度为50μm。3 次迭代后的平均柔顺性相对变化小于 10 -5并且满足所有约束时，假设达到优化收敛。

作为对照，没有执行任何打印约束的合规性最小化。获得的合规值C=345兆焦耳。优化需要 133 次迭代才能收敛。这种配置的打印模拟显示有严重的铺粉结构碰撞，与基板分离后，参考点的整体变形量为 0.61 mm。

为了展示优化能力，设计了优化组合。首先，对铺粉机构碰撞约束进行优化。接下来是针对不同值的四种优化在施加载荷的节点上规定了全局变形约束。最后，对四个不同的值进行优化，结合铺粉机构碰撞约束就完成了。

这些优化的约束值如下表

铺粉机构碰撞拓扑优化：

当新沉积层的顶部节点行在打印方向上向上扭曲，超过临界值时，就会发生铺粉机构碰撞。层厚度t=50μm，相对粉末密度ρpwdr假设等于 50%，碰撞阈值dw根据方程式已设置为100μm。参数r在等式中设置为 25，并且所有层的约束已聚合为单个值。

给定单元高度为 1 mm，层厚为50μm, 20 层集中在单行元素中用于失真分析。对于每一行元素的沉积，需要单独的解决步骤。因此，对于所考虑的支架，每个 AM 打印模拟总共需要 80 个步骤。

从完整的打印模拟中可以看出，仅从合规性最小化获得的设计将导致下图中描绘的节点的铺粉机构碰撞。

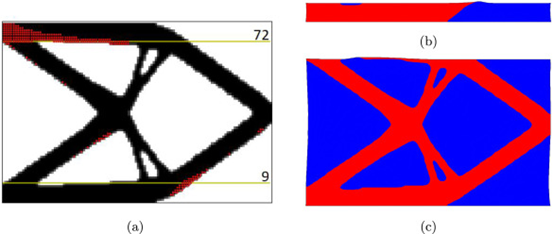
通过拓扑优化从合规性最小化与铺粉机构碰撞约束设计如下图

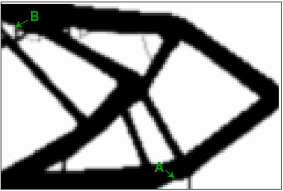
先前发生碰撞的结构底部构件在部件开始上升的位置（用 A 标记）变得更薄。减少发生碰撞的层的水平长度可以防止碰撞，因此材料已被移除。此外，还引入了一个额外的小柱子，将其连接到基板。由于它与左边缘没有连接，它的唯一功能是通过添加机械支撑来限制打印过程中的变形。所有外部构件的宽度都略有减小，并引入了额外的内部构件。顶部构件上层的水平长度已通过改变倾斜角而缩短，这会导致顶部边缘更短，并有一个从下方切入的空隙区域（用 B 标记）。在该区域也可以观察到一些内部支撑材料。此外，由于畸变分布不均匀，部分的垂直对称性已被破坏。内部支撑位置已经改变，以补偿碰撞约束应用程序引入的变化的影响。

在 180 次迭代后获得收敛，最终柔顺性等于 363 mJ，比参考情况高 5.2%。计算时间为 41 分钟和 6 秒，几乎是参考案例的 6 倍。这是因为单次优化迭代现在需要 80 步打印模拟和伴随灵敏度计算，以及单步合规性模拟。约束图表明在优化的早期迭代期间发生碰撞，但之后几乎没有违反约束。100 次迭代后的小峰值表明设计违反了约束，并且解决方案在几次迭代中处于不可行空间中。当约束处于活动状态时，这对于具有非线性约束的优化问题并不罕见。为所有优化迭代保留未显示的体积约束。

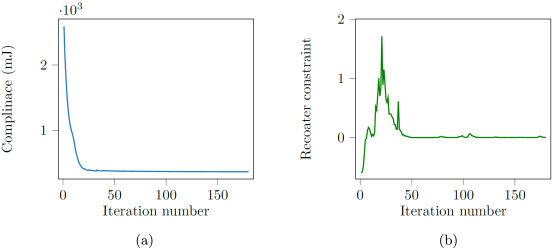
全局失真拓扑优化：

打印变形包含节点层的热收缩以及打印阶段所有后续层的热收缩。由于工件固定到基板上，而受到约束的热收缩会产生残余应力。因此，当零件从基板上释放时，这些残余应力会产生额外的变形。

针对无约束对比件产生的0.61mm变形分别在加载点以dmax等于 0.5、0.2、0.1 和 0.05 毫米优化。

优化结果如下表

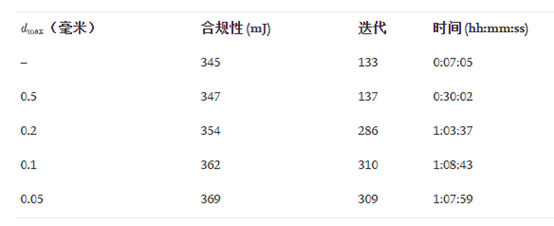
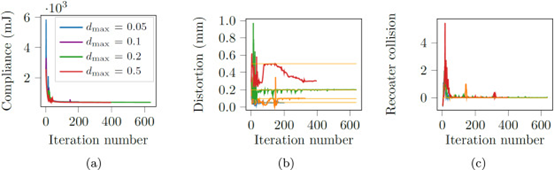
下图展示了不同全局失真约束情况下的顺从性和约束的演变。合规图几乎重叠，这表明相似的收敛行为。在失真约束图中，可以在所有图的早期迭代中观察到一些特征峰值。经过 50 次迭代后，变得平滑。

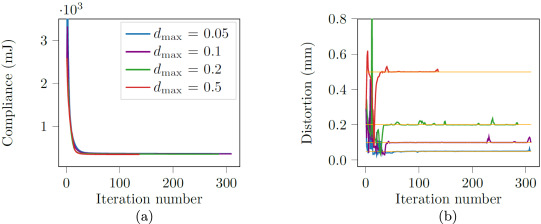
通过下图可以观察到，随着允许变形水平的降低，底部构件变得更直和更薄，而内部构件的数量增加，因此几何复杂性增加。随着约束越来越严格，底部构件变得笔直，与基板板几乎没有连接。以这种方式，释放期间产生的变形被减少，因为释放的反作用力所累积的自由度的数量较少。与没有打印限制的纯合规结果相比，这些设计具有更复杂的拓扑结构，并且垂直对称性被打破。

约束值dmax=0.05mm的模拟打印，零件从基板释放后X方向和Y方向的位移如下图

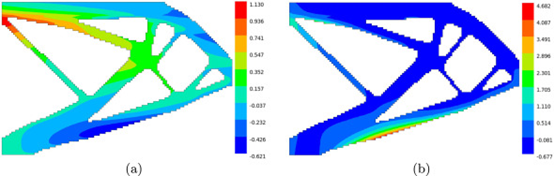
其中密度低于 0.8 的元素被删除，以便显示结构的相关位移。该图确认受约束的左上角节点以及施加力的节点位于预期位置。不包括在约束中的大部分结构显示变形超过 0.05 毫米，甚至高达 4.7 毫米。

热处理的影响因素：

打印件如果热处理后再从基板上释放，通常残余应力会得到缓解。这种情况的优化仅模拟构建阶段而不模拟释放阶段的优化。对于包括释放阶段变形的模拟，在最终释放步骤中，由于从基板释放，变形从超过 0.15 mm 下降到 0.05 mm。如果在释放阶段（即假设热处理）期间没有变形的模拟情况下，受约束节点的变形从第 55 个构建步骤开始保持不变，而在最终增量中，仅应用到装配位置的转换。因此，这两种情况（即热处理和不热处理）导致采用不同失真减少机制的不同设计。

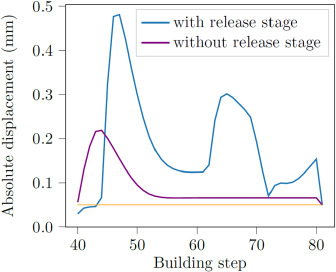
上图最后一步 (81) 代表从基板上释放。橙色线表示允许的失真。

铺粉机构碰撞与全局失真相结合的拓扑优化：

dmax分别为0.05 和 0.1、0.2 和 0.5 毫米，dw=100μm。

获得的合规值和优化数据如下表

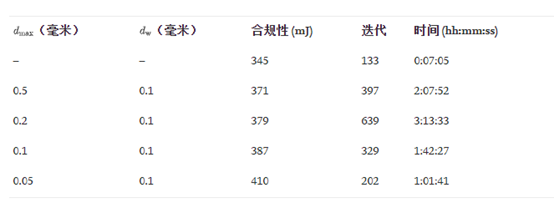
目标和约束历史图表明，在开始时，优化器在保持在可行空间（图中的尖峰）方面存在问题，但经过 200 次迭代后，图相当平滑。目标函数的最大下降发生在前几十次迭代中。此外，优化总是收敛到一个可行的解决方案。

两种优化后结合的结构如下图

构件厚度的不规则性比以前更加明显。出现了许多将零件与基板连接或将构件本身互连的薄结构。这些结构类似于通常用于 3D 打印的支撑结构。许多支撑仍然是灰色的，即具有中等密度值，这表明在这种情况下不需要固体材料的全部刚度来实现所需的减少变形效果。零件本身的承载构件已经收敛到清晰的实心/空心布局。

在X方向和Y方向的位移图如下

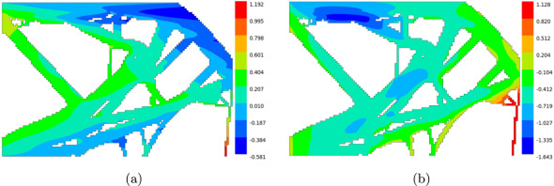
证实了受约束的节点保持在原位（在允许的公差范围内）。右下角的薄支撑出现最大的扭曲由构件底部释放阶段引起的，因此，它会沿逆时针方向弯曲。这种支撑变形不会影响全局变形约束，因为它旨在控制组装配置中的加载节点位置。与没有铺粉机构碰撞约束的情况相比，整体零件变形更小。原因是铺粉机构碰撞约束是影响所有层的约束，因此减少了整个结构的变形。

网格尺寸的影响因素：

网格尺寸0.5X0.5毫米和0.25X0.25毫米，分别得到240 × 160 和 480 × 320 元素离散化的域。

铺粉机构碰撞约束的研究中发现，随着分辨率的增加，发生碰撞的区域减小。这是因为随着元件尺寸的减小，更少的层集中在单个元件层中，这导致在单个步骤中沉积的固有应变能更小，从而降低增量位移。零件从基板释放后节点的变形中，120×80、240×160和480×320单元的域分别为0.61 mm、0.67 mm和0.69 mm的位移，差异不大。

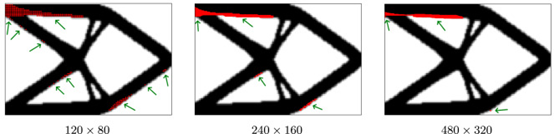
无论有没有铺粉机构碰撞约束，节点的最终变形都被限制为 0.05 mm。没有铺粉机构碰撞约束的优化需要 309、276 和 191 次迭代才能收敛，而带有铺粉机构碰撞约束的优化需要202、234 和 184 次迭代。有趣的是，随着分辨率的增加，具有铺粉机构碰撞约束的设计开始类似于仅具有失真约束的设计。这是因为随着网格分辨率的增加，铺粉机构碰撞约束变得不那么重要。

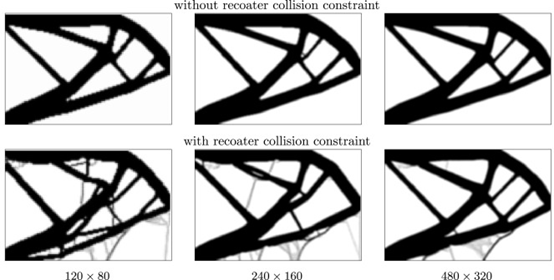
3D示例

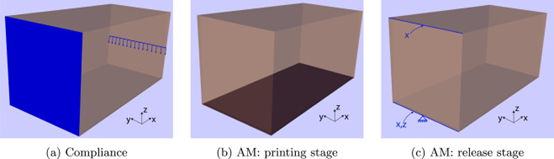
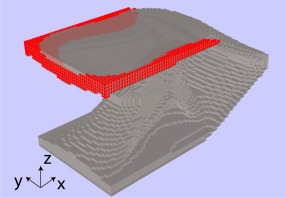
用于优化的设计域由 1X 1X 1 mm 标准三线性六面体单元由 80X40X 40 个单元组成，采用高斯积分方案。左侧支撑结构的柔度最小化，载荷沿穿过右侧中间的水平线垂直施加（见下图(a)）。在打印阶段，底部被完全约束（见下图 (b)) 并且在释放阶段左下边缘被限制在X和Z方向，顶部边缘被限制在X方向和左下边缘的中间节点被完全抑制（见下图（c））。

粉末材料是 Ti6Al4V，具有与 2D相同的特性，模拟中应用的固有应变为

?inh=(0.00299,0.00299,0,0,0,0)

最大体积分数设置为 40%，密度过滤器半径设置为 1.5 mm。再次将收敛标准设置为目标函数在过去 3 次迭代中平均的相对变化低于 10 -5。

采用3种优化组合，第一个是铺粉机构碰撞约束。优化dmax设置为 0.1 毫米。全局变形约束的公式化使得它将所有加载节点的变形限制为dmax。因此，加载节点的变形被收集到一个单一的P规范函数

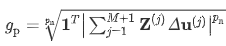
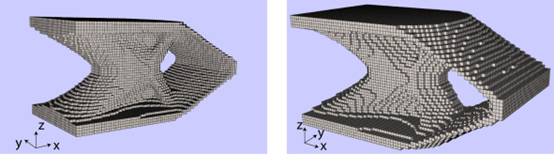
最大范数Pn=7

与 2D 示例相比，所需的迭代次数大致相似。然而，计算时间显著增加。

由于所考虑的建模方法中的层添加可以独立计算，因此并行解决方案可以将计算时间减少至少 10 倍。

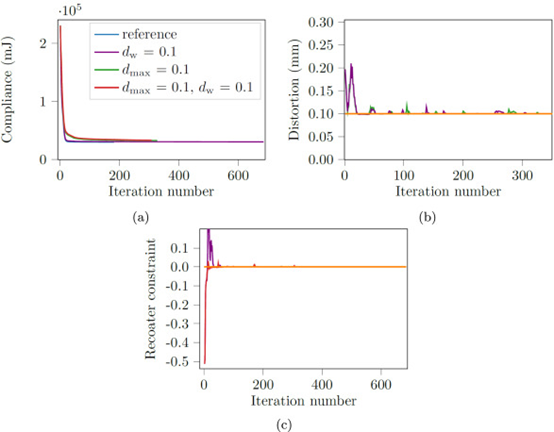
大多数目标函数减少发生在前 50 个增量中，失真和碰撞约束的跳跃也是如此。这表明可以放宽应用的收敛标准以减少计算时间。大多数迭代都保留了约束，它们的迭代历史类似于二维优化收敛图中的那些。

铺粉机构碰撞拓扑优化：

必须发生与 2D 相同的条件才能发生铺粉机构碰撞。所以，dw被设定为100μm。参数r设置为 25，并且所有层的约束已聚合为单个函数；由于域高度为 40 个元素，因此收集了 40 个单独的沉积步骤。下图参考形状的打印模拟表明，用红点标记的节点发生了碰撞。总共有 2153 个节点违反了约束，并且可以观察到它们都位于结构的顶部。失真度最高的Z 方向为 0.33 毫米，超过了阈值。

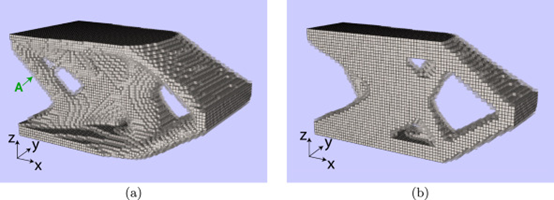
应用铺粉机构碰撞约束获得的设计如下图所示。与对比案例相比，内部构件的形状更复杂，零件的Z方向对称性破坏了。添加了额外的构造，用 A 标记，以支持对比设计中发生碰撞的结构顶部。结构的正面几乎没有变化，这是符合预期的，因为打印模拟显示该区域没有铺粉机构碰撞。

全局失真拓扑优化：

约束节点最大变形为 0.66 mm，允许的最大失真被设置为 0.1 mm。在图 24中，只有密度大于或等于 90% 的元素被绘制为完整元素，而透明元素是那些密度在 20% 和 90% 之间的元素。

优化器提出了中空结构，在设计域的角落引入了两个完全密集的柱子，作为支撑。可以对照2D示例中对应设计图。

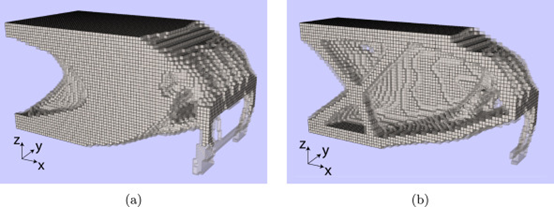
铺粉机构碰撞与全局失真约束相结合：

可以观察到具有向左侧移动的较薄内部构件的壳状中空结构。出现了更复杂的支撑结构，这与应用两个约束的情况下在二维中观察到的趋势相匹配。在结构从基板开始上升的位置附近引入了一个小柱子。

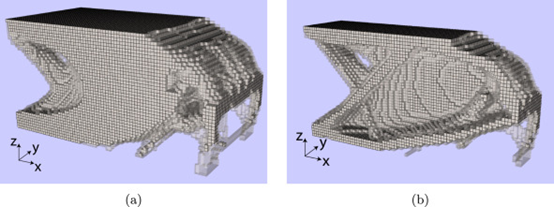
至此，已经内容介绍了两种不同的生产约束：防止铺粉机构碰撞和约束整体形状变形。优化设计生成了许多辅助支撑结构，旨在促进生产，而不是提高零件结构性能。此外，已经表明，在打印阶段产生的变形可以通过部件从底板释放时产生的额外变形来补偿。

该方法的适用性和有效性已在 2D 和 3D 中进行了说明。3D 中支架的优化（包括所提出的失真约束）的特点是创建了盒状结构，这与传统的顺应性最小化结果中看到的庞大的中央结构形成对比。3D 的总优化时间在几天的范围内，这仍然是合理的，因为它涉及瞬态数值模型。

将增材制造约束添加到基于 SIMP 的拓扑优化中，预计会导致合规性目标适度增加 4% 到 29%，具体取决于约束的严格程度。

鉴于在设计或打印过程的后期阶段失败的高昂成本，以上优化是完全有必要的。